kNN概述

机器学习算法：

机器学习算法分为两类：懒惰和急切学习。懒惰学习算法包括存储训练数据并在接收到新的输入数据时计算一些结果，而急切训练包括预先计算算法并将其用于新的输入数据。这些可以进一步划分为有监督或无监督学习。监督学习要求测试数据已经预先分类，而无监督学习则没有。

分类：

分类是一种有监督且通常懒惰的学习方法。一般来说，这个过程分为两个阶段：培训和分类。培训阶段包括将预先分类的数据输入模型，以开发可在分类阶段使用的数据集。分类阶段包括将新的，未分类的数据输入到训练模型中并尝试为其添加新标签。流行的分类算法包括Naive Bayes，支持向量机以及最近邻算法。

kNN算法：

我们的项目侧重于实现k-Nearest Neighbor（kNN）算法。与大多数分类器一样，该算法在训练阶段接收预先分类的数据。在分类阶段，算法确定新测试数据与整个训练集之间的距离，并查看k，用户定义的常数，最近邻居，并选择发生率最高的邻居。换句话说，我们可以将算法分为三个主要阶段：距离计算，排序和选择。

kNN算法

高级设计：

kNN硬件的设计包括三个主要模块：距离计算器，分拣机和选择器。

管道：

我们的分类器管道包括单周期距离计算器，单周期分拣机和k循环选择器。换句话说，分类器从我们的训练集接收分类数据块以及新的测试数据块，并在一个周期中将其放置在重新排序的列表中时计算距离。该算法对训练集中的每个数据块执行该计算，因此需要n个周期来计算新的测试数据块与我们的训练集中的n个分类数据块之间的距离。之后，我们的管道需要k个周期来查看排序列表中的k个最近邻居，并将其输出为我们测试块的新标签。

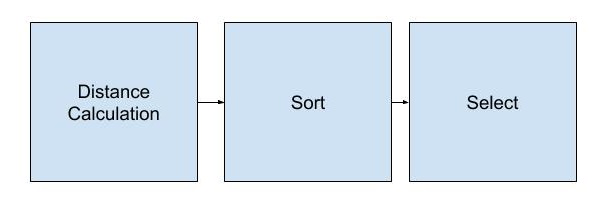
图：管道

这个kNN管道专门用于图像识别，专门用于我们如何编码图像。如上所述，我们已决定将图像编码为64,16位字，其充当强度直方图。将其映射到我们的硬件，我们的距离计算器包括对训练数据块的64个字中的每个字与新测试数据块之间的差异求和。我们的排序包括获取计算的距离并维护所有训练数据块的排序列表。我们的选择器查看排序列表中的前k个元素并输出最高的元素。

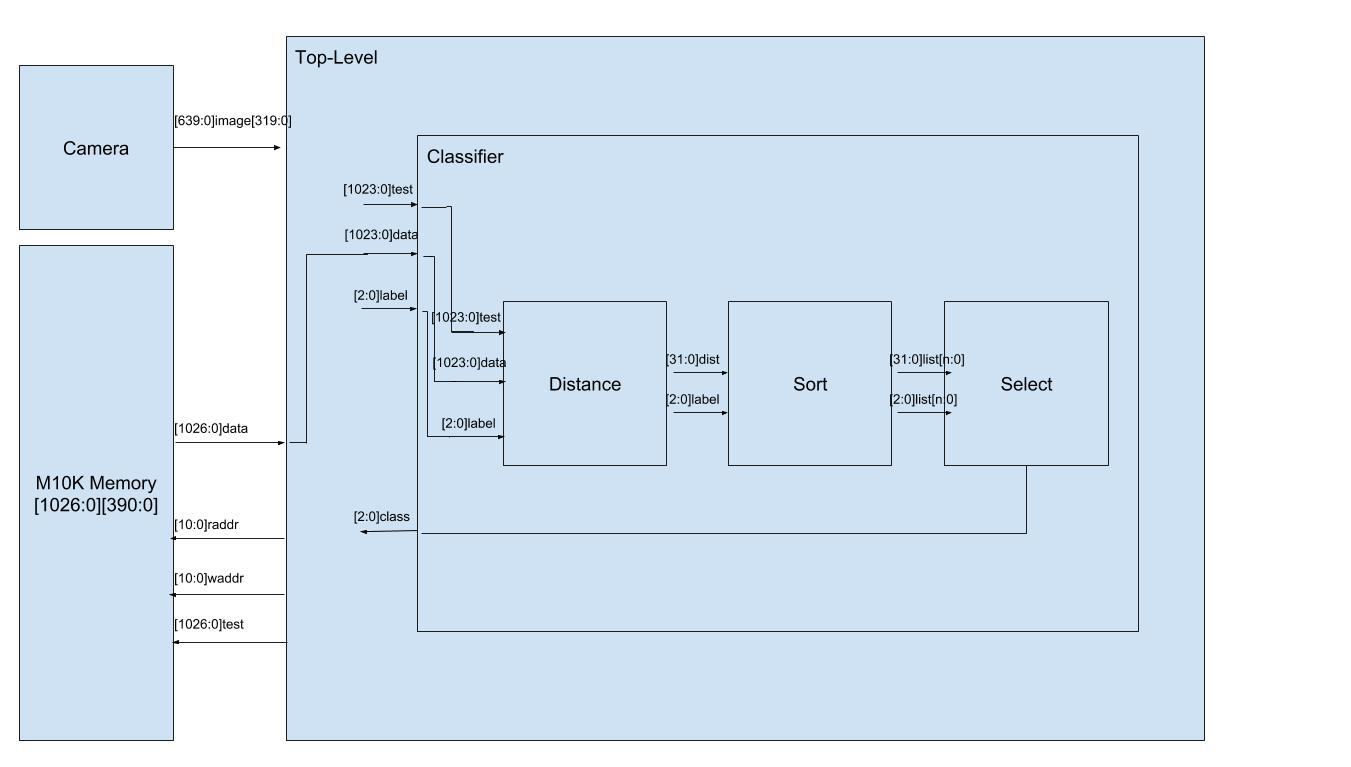
图：框图

距离：

距离计算器经历了许多次迭代设计。第一个设计涉及一个12周期管道，以减少使用的加法器总数，并希望允许更多的并行化。在对该设计进行了一些初步测试之后，我们转向了单周期组合设计，因为用于处理状态的额外逻辑单元占用了比预期更多的空间。最终距离模块简单地为训练数据和测试数据提供64位，16位字，两者均表示为1024位输入，并行执行64次减法，然后进行60次加法。

分类：

排序算法也经历了多次迭代。最初的设计涉及每个数据的两个周期/两个阶段。第一个周期旨在决定新数据的去向，以及为了容纳新数据而必须移位哪些数据，第二个周期是在正确的位置解决所有数据。我们挑战自己改进设计。这一挑战背后的主要动机是数据被串联送入分拣机，我们的主要目标是显示现有算法的硬件加速。最终实现在单个周期中对传入排序模块的数据进行排序，确定新数据所属的位置以及如何在同一周期中替换先前的数据。

分拣机的最终实施部分源于我们在之前的实验室中实施的鼓式合成器。鼓合成器具有代表鼓上节点的单元，并且可以访问关于其相邻单元的信息，这是确定其下一个值所必需的。类似地，分拣机由一组桶模块组成，这些模块是为了在数据进入时正确对数据进行分类而生成的。桶中包含有关新数据的信息，自身的状态和值，以及状态和数据。上面的桶。

每个桶模块有bucket_data寄存器来存储数据，并且bucket_full注册跟踪的状态（满或空）。这两个寄存器都连接到桶模块的输出。铲斗模块的输入是时钟，重置，和使能，以及NEW_DATA代表进来的数据输入，以及above_data和above_full分别跟踪数据和状态上述铲斗的。

在每个时钟周期，存储桶将决定存储哪些数据。每个桶最初（并且在重置时）设置为空并且具有存储值“0”。如果上面的桶是空的，桶没有存储任何东西，并保持空。最上面的桶将above_full输入硬连接到full，并且above_data输入硬连接到0（最小的欧几里德距离）。如果当前桶为空，则上述桶已满，上述桶数据不大于新数据，桶存储新数据。如果当前桶数据大于新数据且上述桶数据不是，则桶也存储新数据。但是，如果上述存储桶数据在任何时候都大于新数据，则当前存储桶始终存储上述存储桶数据。

选择：

选择模块是整个过程的瓶颈。在对所有数据进行排序后，选择器必须查看前k个数据并选择哪个标记最常见。换句话说，选择器将选择在与给定图像具有最小距离的图像中最常表示的标签 - 选择k个最近邻居的模式。选择器等待分拣机完成，迭代通过每个前k个数据块一次，然后，在下一个循环中，确定它们中最常出现的标签。我们还改进了设计，使选择器不仅输出选择，而且还以最多k个匹配数据集的形式输出置信度。

图：选择的百分比准确度

设计结果

性能和加速：

最终设计在性能方面有了很大的提升。设计的第一次迭代涉及使用PIO引脚将图像直方图传递给HPS，然后HPS将运行kNN分类器。在性能计算方面，对于每个图像，此设计需要迭代64个元素阵列并执行减法，否定和滚动添加，然后执行内存写入。换句话说，我们将有两个主要的for循环，它们将编译成至少512个ARM指令（不计算跳转和控制流逻辑）。在此之后，我们必须对数组进行排序，即O（nlogn）就图像的数量而言，就指令而言，这可以变化，但至少是元素的数量乘以其日志。最后，它必须重复并计算相对于所选择的k 的最近邻，即O（k）。换句话说，我们将至少采用（512 + 896）* n + k个周期，其中n是存储在存储器中的面数，k是所选择的k。

相比之下，FPGA计算距离并在1个周期内保持排序列表，然后需要k个周期进行选择。换句话说，我们采用有界n + k个循环，其中n是图像的数量并且选择k。正因为如此，我们预测原始周期的加速速度约为1000倍，而FPGA的时钟速度则较慢。得到官方结果后，我们看到分类器在HPS上以800000 MHz的频率拍摄了9680个周期，10个图像的k值为10，而FPGA在相同的测试中花费了20个周期但是在FPGA的50000 MHz时钟。运行100个图像时，HPS的周期数呈指数增长，达到6500000个周期，而FPGA需要110个周期。换句话说，当FPGA线性增加时，我们看到HPS的计算时间呈指数增长。

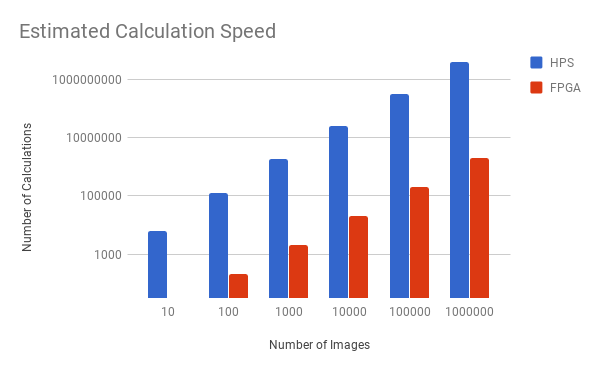
图：分类器速度

在准确性方面，模型按预期执行。换句话说，准确度会根据您训练模型的程度呈指数级增长。我们设计的第一次迭代允许存储最多100个图像。对于面部识别，我们看到假设背景图像保持相对相似，每张脸约有25张图像保证接近完美的结果。最终编译的设计最多允许存储300个模型，这样可以获得更高的精度。作为基准，似乎每个分类至少保存了25个图像，准确率达到99％左右。

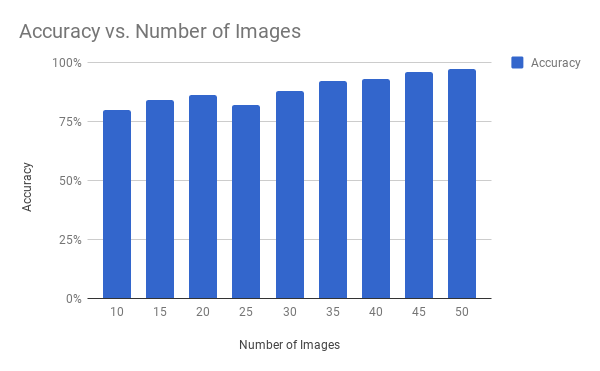
图：分类器的准确性

除了遵循一般正确的编码程序以确保没有意外或未定义的行为之外，确实没有安全考虑因素。在使用方面，我们看到用户界面相对容易遵循。我们让Key 3捕获了一个新图像，并将标签分配为Switch 6，Switch 5，Switch 4. Key 2将尝试对新的图像捕获进行分类。并且Key 0充当重置。我们有很多同行尝试我们的项目，所有人都回答说它非常直观。

分类：

距离计算器的原始设计包括12周期流水线距离计算。这是为了防止大型扇出实例化64个减法器和60个加法器，并将这些减法器连接起来进行1个周期的计算。最初的设计有一个稍微复杂的管道，其中12个循环流水线距离计算器将被实例化，并且将有一个仲裁器用于决定在每个周期使用哪个距离计算器。最终，这两种设计将导致类似的吞吐量（假设具有相同的并行化水平），同时节省了几个潜在的加法器，并且还大幅减少了扇出。然而，二次设计最终证明要好得多。

分拣机和选择器：

分拣机和选择器都经历了多次迭代。最棘手的部分是平衡单周期分拣机的复杂性，并保持设计“轻量化”以保护ALM，以防项目其他部分需要它们。分拣机桶模块的许多迭代具有来自其他桶的更多输入并且包含多个寄存器。在设计中使用寄存器总是增加了必要周期的数量，并使设计更加复杂。排序的最终解决方案非常优雅，并且尽可能少地使用铲斗模块之间的互连。选择器的设计较少涉及，但是，由于Verilolg中迭代器的繁琐性，需要花费相当多的时间来测试。作为测试选择器模块的一部分，我们检查了前几个k的数量邻居与所选结果相匹配。我们决定将这些信息保存为我们向用户“冒泡”的内容，以查看匹配的接近程度，并可能决定是否需要更多地训练算法。

由此产生的分类和选择设计在硬件上远远快于其软件对应物。即使是最好的排序算法也具有复杂度O（nlogn），而我们的最差情况时序恰好为n。排序在n个循环中完成，其中n是训练集的大小。关于分类图像的决定是在k + 1个循环中达到的，其中k是所选择的最近邻居的数量。

结论

评论：

在我们的项目中，我们开始在FPGA上构建kNN算法，以展示硬件加速如何帮助机器学习算法实现仅使用软件无法找到的速度。我们发现我们的硬件实现明显快于我们的软件实现，这与我们期望看到的结果相匹配。我们还试图在识别器上实现合理的准确性，并且只要对象的背景类似于之前看到的那个，分类器就非常准确。该设备在尝试在全新背景中找到已经分类的对象时不是最有效的，但如果它被用作纵向分析器，例如在完全白色的背景上，则可以可靠地正确地对图像进行分类。如果我们要重做项目，我们可能会寻找其他方法来专门化项目，例如，将图像存储在硬件上，以便我们可以执行复杂的数学运算，例如梯度分析，以便对面部进行分类。然而，这种专业化将以功能或空间为代价，因为我们用于合理规模的项目实施的开发板上几乎没有足够的空间。